Reaksi Tumpuan akibat beban terpusat.

Bahan Ajar 1

Sarmulia Sinaga,ST.,MT.

Widyaiswara Ahli Madya

PPPPTK Bidang Bangunan dan Listrik Medan

I.     Reaksi Tumpuan akibat beban terpusat.

1.1.  Reaksi Tumpuan akibat 1 beban terpusat.

Banyak hal yang terjadi pada konstruksi kita yang diidealisasikan menjadi sebuah balok. Walaupun secara konsep hal ini harus menggunakan anggapan dan asumsi dalam perhitungan untuk menyederhanakannya. Dalam penyederhanaan ini, kita harus memahami dan menyepakati beberapa lambing dan symbol yang digunakan. Setelah diidealisasikan, diperoleh sebuah balok sederhana dengan panjang bentangan L seperti diperlihatkan pada gambar 1.1 di bawah ini

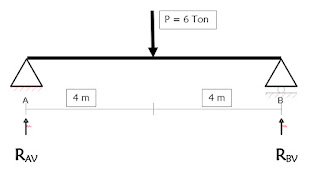
Gambar 1.1  Reaksi Tumpuan pada balok sederhana yang dibebani dengan beban terpusat P

Untuk memulai perhitungan, kita melihat tumpuan pada ke dua perletakan yang dianggap sebagai Sendi (A) dan Rol (B).Perlu dipahami bahwa sendi dan rol tidak dapat memikul momen. Perletakan sendi dapat memikul dua gaya yang terjadi, yaitu gaya vertikal dan horizontal sementara pada perletakan  rol hanya dapat memikul gaya vertical saja. Oleh sebab itu, untuk menghitung reaksi yang terjadi kita mulai bergerak dari nilai momen yang terjadi di titk B adalah Nol, maka :

∑M_B = 0

Lankah berikutnya adalah : semua gaya yang bekerja pada balok dimomenkan ke perletakan B harus Nol, (kita sepakati arah putaran searah jarum jam) maka :

Atau, dapat juga sebaliknya, untuk menghitung reaksi yang terjadi kita mulai bergerak dari nilai momen yang terjadi di titk A adalah Nol, (kita sepakati arah putaran searah jarum jam) maka :

∑M_A = 0

Lankah berikutnya adalah : semua gaya yang bekerja pada balok dimomenkan ke perletakan A harus Nol. 

-RA . L + P . a = 0

RA = PA/L

Dimana :

R_A      =   Reaksi Perletakan di titik A

R_B      =   Reaksi Perletakan di titik B

a       =  Jarak beban terpusat dari perletakan A

P       =  Beban terpusat

L       =  Panjang bentangan

1.2.Reaksi Tumpuan akibat  beban terpusat majemuk.

Banyak hal yang terjadi pada konstruksi kita yang diidealisasikan menjadi sebuah balok seperti materi ini, misalnya ; Balok dengan balok anaknya pada plat, kendaraan yang melintas di atas jalan atau jembatan dan setarusnya . Walaupun secara konsep hal ini harus menggunakan anggapan dan asumsi dalam perhitungan untuk menyederhanakannya.

Kita idealisasikan konstruksi tersebut seperti gambar 1.2 berikut ini :

Untuk memulai perhitungan, kita melihat tumpuan pada ke dua perletakan yang dianggap sebagai Sendi (A) dan Rol (B).Perlu dipahami bahwa sendi dan rol tidak dapat memikul momen. Perletakan sendi dapat memikul dua gaya yang terjadi, yaitu gaya vertikal dan horizontal sementara pada perletakan  rol hanya dapat memikul gaya vertical saja. Oleh sebab itu, untuk menghitung reaksi yang terjadi kita mulai bergerak dari nilai momen yang terjadi di titk B adalah Nol, maka :

∑MB = 0

Lankah berikutnya adalah : semua gaya yang bekerja pada balok dimomenkan ke perletakan B harus Nol, (kita sepakati arah putaran searah jarum jam) maka :

                                                    1.3

Atau, dapat juga sebaliknya, untuk menghitung reaksi yang terjadi kita mulai bergerak dari nilai momen yang terjadi di titk A adalah Nol, (kita sepakati arah putaran searah jarum jam) maka :

1.4

Dimana :

R_A    =   Reaksi Perletakan di titik A

R_B    =   Reaksi Perletakan di titik B

a     =   Jarak beban terpusat P₁ dari perletakan A

b     =  Jarak beban terpusat P₂ dari perletakan A

P₁, P₂  =  Beban terpusat

L     =  Panjang bentangan

Perhitungan dapat dikontrol untuk memastikan hasil perhitungan reaksi pada tumpuan sudah benar  dengan cara memperhitungkan reseltan gaya vertical harus nol, maka :

1.3.     Reaksi Tumpuan akibat  beban terpusat majemuk dengan sudut tertentu.

Pada kasus ini secara prinsip perhitungan sama saja dengan kasus di atas,  hanya saja kita perlu memproyeksikan gaya yang bekerja menjadi gaya vertical dan horizontal. Untuk lebih memahami, mari kita amati gambar 1.3  berikut ini:

Proses penyelesaian kasus ini tidak berbeda dengan dua kasus di atas, dengan syarat kita harus memproyeksikan gaya – gaya yang membentuk sudut menjadi gaya vertical dan gaya horizontal. Untuk melakukan perhitungan, kita melihat tumpuan pada ke dua perletakan yang dianggap sebagai Sendi (A) dan Rol (B). Perlu dipahami bahwa sendi dan rol tidak dapat memikul momen. Perletakan sendi dapat memikul dua gaya yang terjadi, yaitu gaya vertikal dan horizontal sementara pada perletakan  rol hanya dapat memikul gaya vertical saja. Oleh sebab itu, untuk menghitung reaksi yang terjadi kita mulai bergerak dari nilai momen yang terjadi di titk B adalah Nol, maka :

∑MB = 0

Lankah berikutnya adalah : semua gaya yang bekerja pada balok dimomenkan ke perletakan B harus Nol, (kita sepakati arah putaran searah jarum jam) maka :

RAv.L – P₁(L-a) – P₂(L-b) – P3 Sinα( L-c) = 0

             P₁(L-a) – P₂(L-b) – P3 Sinα( L-c)

R_A       =   -------------------------------------------------

                        L

Atau, dapat juga sebaliknya, untuk menghitung reaksi yang terjadi kita mulai bergerak dari nilai momen yang terjadi di titk A adalah Nol, (kita sepakati arah putaran searah jarum jam) maka :

∑MA = 0

-RB . L + P2.b + P1.a+ P3 Sinα .( c ) = 0

              P2.b + P1.a+ P3 Sinα .( c )

R_B       =    --------------------------------------

                     L

Dimana :

R_A        =   Reaksi Perletakan di titik A

R_B         =   Reaksi Perletakan di titik B

a         =  Jarak beban terpusat P₁ dari perletakan A

b        =  Jarak beban terpusat P₂ dari perletakan A

c         =  Jarak beban terpusat P3 dari perletakan A

P₁, P₂ ,P₃  =  Beban terpusat

α         = Sudut gaya P₃ dengan Bidang datar 
L         =  Panjang bentangan

Daftar Pustaka

1.
E.L.Wilson, SAP2000® Integrated Finite Element Analysis and Design of Structures : CONCRETE DESIGN MANUAL, Computers and Structures, Inc. Berkeley, California, USA, Version 7.40 May 2000.
2. Soemoni,Ir.Prof. Ilmu Gaya Bangunan-bangunan Statis tertentu,Djambatan Jakarta 1993.
3. Karyoto, Mekanika Teknik satis tertentu,Teknik Sipil UNESA, 2013
4. Popov.,E.P. Mekanika Teknik Erlangga Jakarta 1984.